El área y el perímetro de un triángulo son medidas fundamentales en geometría que describen la extensión y el contorno de esta figura básica. Aquí te presento una guía detallada sobre cómo calcular ambas propiedades para diferentes tipos de triángulos.
Área del Triángulo
El área de un triángulo puede calcularse de varias maneras dependiendo de la información disponible.
Fórmula Básica
Para un triángulo con base bb y altura hh:

Fórmula de Herón
Para un triángulo con lados aa, bb y cc, primero se calcula el semiperímetro ss:
s=a+b+c2s = \frac{a + b + c}{2}
Luego, el área AA se calcula como:
A=s(s−a)(s−b)(s−c)A = \sqrt{s(s-a)(s-b)(s-c)}
Ejemplo:
Si un triángulo tiene lados de 7 cm, 8 cm y 9 cm:
- Calcular el semiperímetro:
s=7 cm+8 cm+9 cm2=12 cms = \frac{7 \, \text{cm} + 8 \, \text{cm} + 9 \, \text{cm}}{2} = 12 \, \text{cm}
- Calcular el área:
Perímetro del Triángulo
El perímetro de un triángulo es la suma de las longitudes de sus tres lados.
Fórmula
Para un triángulo con lados aa, bb y cc:
Perıˊmetro=a+b+c\text{Perímetro} = a + b + c
Ejemplo:
Si un triángulo tiene lados de 5 cm, 12 cm y 13 cm:
Perıˊmetro=5 cm+12 cm+13 cm=30 cm\text{Perímetro} = 5 \, \text{cm} + 12 \, \text{cm} + 13 \, \text{cm} = 30 \, \text{cm}
Casos Especiales
Triángulo Equilátero
Un triángulo equilátero tiene todos sus lados iguales (a=b=ca = b = c) y todos sus ángulos son de 60 grados.
- Perímetro:
Perıˊmetro=3a\text{Perímetro} = 3a
- Área:
Aˊrea=34a2\text{Área} = \frac{\sqrt{3}}{4}a^2
Ejemplo:
Si un triángulo equilátero tiene lados de 6 cm:
- Perímetro:
Perıˊmetro=3×6 cm=18 cm\text{Perímetro} = 3 \times 6 \, \text{cm} = 18 \, \text{cm}
- Área:
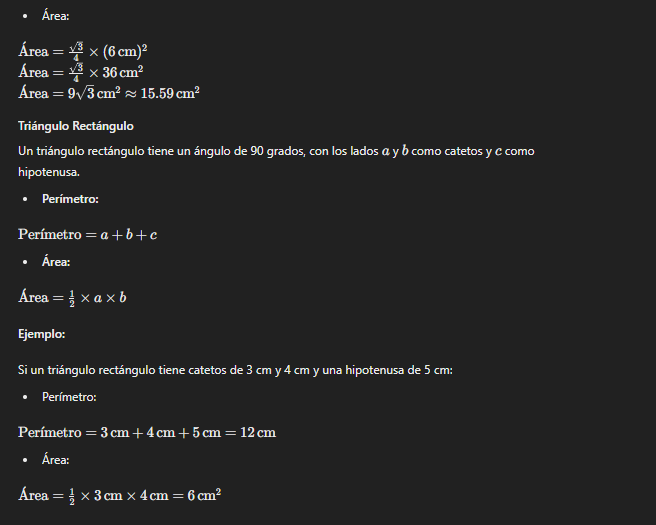
Aˊrea=34×(6 cm)2\text{Área} = \frac{\sqrt{3}}{4} \times (6 \, \text{cm})^2 Aˊrea=34×36 cm2\text{Área} = \frac{\sqrt{3}}{4} \times 36 \, \text{cm}^2 Aˊrea=93 cm2≈15.59 cm2\text{Área} = 9\sqrt{3} \, \text{cm}^2 \approx 15.59 \, \text{cm}^2
Triángulo Rectángulo
Un triángulo rectángulo tiene un ángulo de 90 grados, con los lados aa y bb como catetos y cc como hipotenusa.
- Perímetro:
Perıˊmetro=a+b+c\text{Perímetro} = a + b + c
- Área:
Aˊrea=12×a×b\text{Área} = \frac{1}{2} \times a \times b
Ejemplo:
Si un triángulo rectángulo tiene catetos de 3 cm y 4 cm y una hipotenusa de 5 cm:
- Perímetro:
Perıˊmetro=3 cm+4 cm+5 cm=12 cm\text{Perímetro} = 3 \, \text{cm} + 4 \, \text{cm} + 5 \, \text{cm} = 12 \, \text{cm}
- Área:
Aˊrea=12×3 cm×4 cm=6 cm2\text{Área} = \frac{1}{2} \times 3 \, \text{cm} \times 4 \, \text{cm} = 6 \, \text{cm}^2
Conclusión
El cálculo del área y el perímetro de un triángulo depende del tipo de triángulo y de la información disponible. Las fórmulas básicas y de Herón permiten encontrar estas medidas con precisión. Comprender estos cálculos es esencial en la geometría y tiene aplicaciones prácticas en la construcción, diseño y otras áreas.
Share the Fun!